CoGr@Ohm

← Beleuchtung | ● | Modellierung von Objekten →

• Die erhaltenen transformierten Punkte beschreiben die Rasterkoordinaten der Dreiecke auf dem Bildschirm. Die Dreiecke werden nun anhand des Bildschirmrasters in Fragmente zerlegt.
• Die Vertexattribute jedes Fragments werden baryzentrisch interpoliert

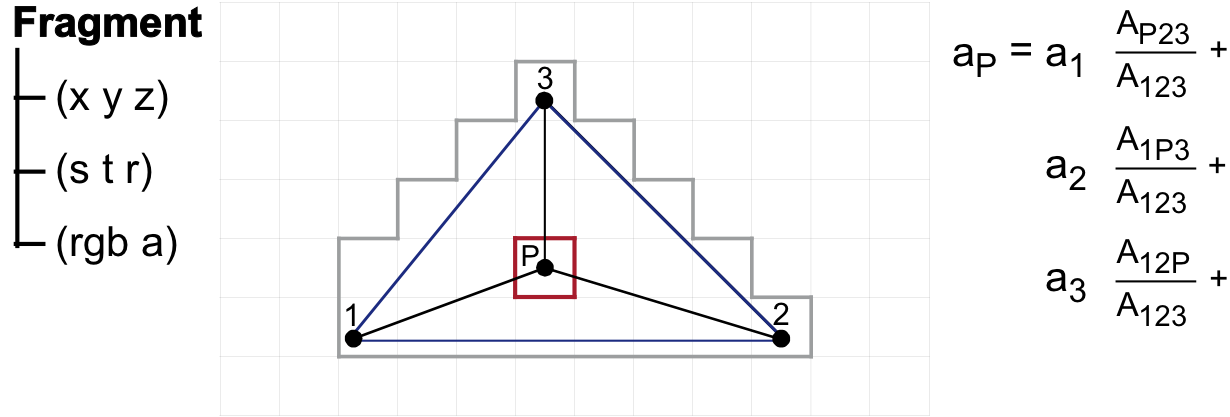
Beispiel 1: Berechnung der Koordinaten des Mittelpunkts eines Dreiecks

Gewichte:

$\frac{A_{P23}}{A_{123}}$, $\frac{A_{1P3}}{A_{123}}$, $\frac{A_{12P}}{A_{123}}$ betragen jeweils $\frac{1}{3} \approx 0,3$ (Begründung: In diesem Sonderfall betrachten wir den Mittelpunkt des Dreiecks)

Eckpunktkoordinaten (2D):

$\vec{a_1} = \left( \begin{array}{c} -2 \\ -1 \end{array} \right)$, $\vec{a_2} = \left( \begin{array}{c} 0 \\ 2 \end{array} \right)$, $\vec{a_3} = \left( \begin{array}{c} 2 \\ -1 \end{array} \right)$

Interpolierter Mittelpunkt:

$\vec{a_P} = \frac{1}{3} \left( \begin{array}{c} -2 \\ -1 \end{array} \right) + \frac{1}{3} \left( \begin{array}{c} 0 \\ 2 \end{array} \right) + \frac{1}{3} \left( \begin{array}{c} 2 \\ -1 \end{array} \right) = \left( \begin{array}{c} 0 \\ 0 \end{array} \right)$

Beispiel 2: Berechnung der Mischfarbe des Mittelpunkts eines Dreiecks

Gewichte:

$\frac{A_{P23}}{A_{123}}$, $\frac{A_{1P3}}{A_{123}}$, $\frac{A_{12P}}{A_{123}}$ betragen jeweils $\frac{1}{3} \approx 0,3$

Eckpunktfarben (RGB):

$\vec{a_1} = \left( \begin{array}{c} 1 \\ 0 \\ 0 \end{array} \right)$, $\vec{a_2} = \left( \begin{array}{c} 0 \\ 1 \\ 0 \end{array} \right)$, $\vec{a_3} = \left( \begin{array}{c} 0 \\ 0 \\ 1 \end{array} \right)$

Interpolierte Mittelpunktfarbe:

$\vec{a_P} = \frac{1}{3} \left( \begin{array}{c} 1 \\ 0 \\ 0 \end{array} \right) + \frac{1}{3} \left( \begin{array}{c} 0 \\ 1 \\ 0 \end{array} \right) + \frac{1}{3} \left( \begin{array}{c} 0 \\ 0 \\ 1 \end{array} \right) = \left( \begin{array}{c} \frac{1}{3} \\ \frac{1}{3} \\ \frac{1}{3} \end{array} \right)$

Der einzige Trick ist also: Wie berechnen wir die Gewichte bzw. Flächeninhalte? Hierzu folgt eine separate Übung zu den Baryzentrischen Koordinaten.

← Beleuchtung | ● | Modellierung von Objekten →