Szenengraphtraversal Rechenbeispiel
← Szenengraphtraversal Beispiel | ● | Szenengraphen →
In der folgenden Blender-Szene ist eine Objekt-Hierarchie dargestellt, in der Translation, Rotation, uniforme Skalierung sowie die View-Transformation verwendet werden:
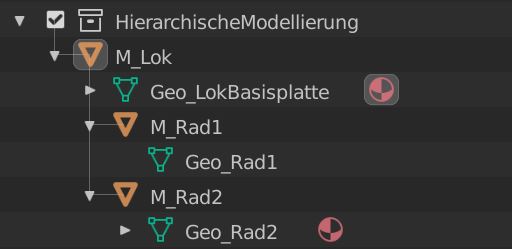
Wir bauen die finale Transformation aus relativen Transformationen $T^{vonKoordinatensystem}_{zuKoordinatensystem}$ und absoluten Transformationen $M_{Koordinatensystem}$ auf.
Wir starten im Weltursprung:
$ M_{Welt} = I $
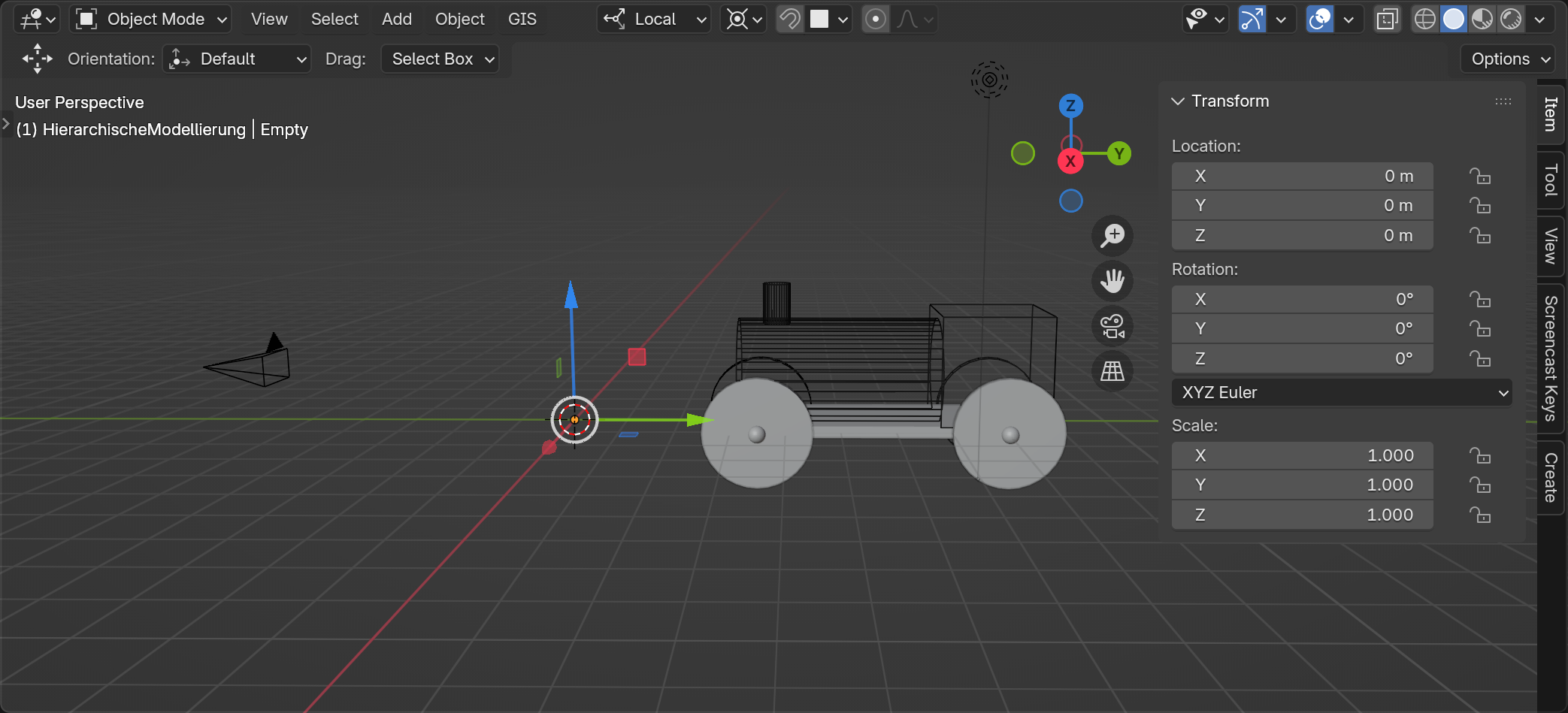
Vom Weltursprung aus bewegen wir uns nun 6 Einheiten entlang der Y-Achse an die Position der Basisplatte der Lokomotive $M_{Lok}$:
$ T^{Welt}_{Lok} = \left( \begin{array}{c c c c} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 6 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{array} \right) $ → $ M_{Lok} = M_{Welt} T^{Welt}_{Lok} $
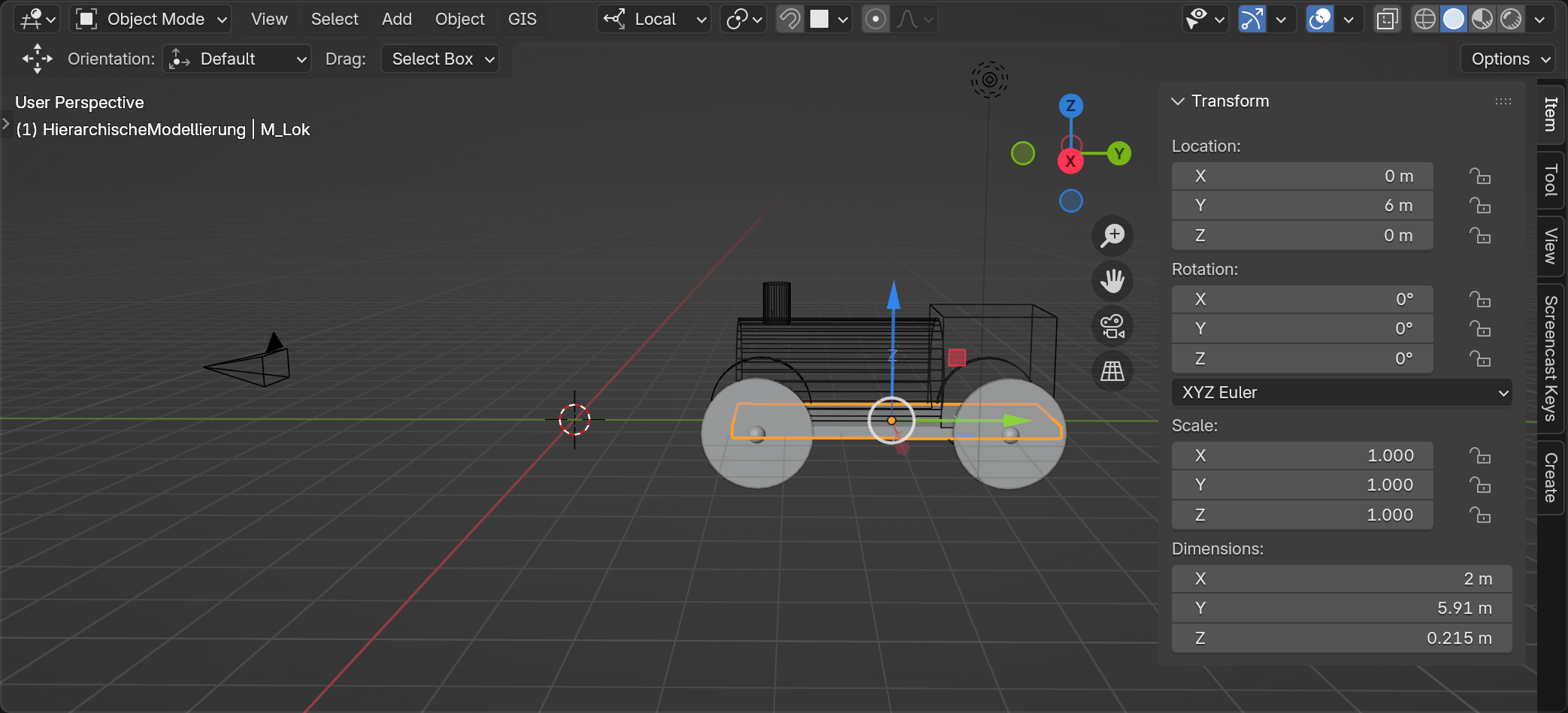
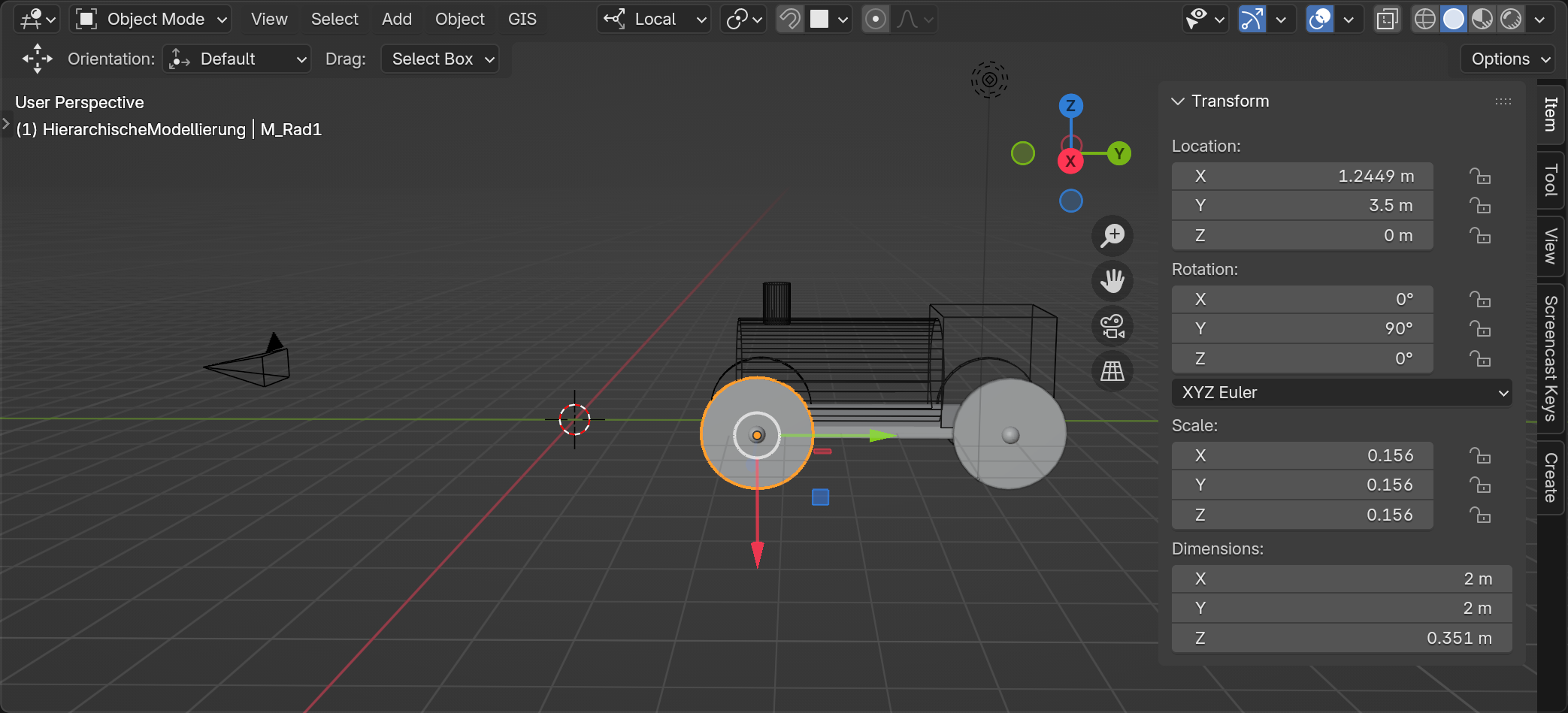
Von der Basisplatte bewegen wir uns nun entweder zum ersten Rad $M_{Rad1}$ indem wir eine Verschiebung um 1,244 Einheiten entlang der X-Achse und −2,5 Einheiten entlang der Y-Achse, eine Rotation von 90 Grad ($\theta = \pi/2$) um die Y-Achse eine uniforme Skalierung s=0,156 modellieren:
$ T^{Lok}_{Rad1} = \left( \begin{array}{c c c c} s \cdot cos(\pi/2) & 0 & s \cdot sin(\pi/2) & 1,244 \\ 0 & s & 0 & -2,5 \\ -s \cdot sin(\pi/2) & 0 & s \cdot cos(\pi/2) & 0 \\ 0 & 0 & 0 & 1 \end{array} \right) $ → $ M_{Rad1} = M_{Lok} T^{Lok}_{Rad1} $
Oder wir bewegen uns von der Basisplatte zum zweiten Rad $M_{Rad2}$ indem wir eine Verschiebung um 1,244 Einheiten entlang der X-Achse und 2 Einheiten entlang der Y-Achse, eine Rotation von 90 Grad (Pi/2) um die Y-Achse eine uniforme Skalierung s=0,156 modellieren:
$ T^{Lok}_{Rad2} = \left( \begin{array}{c c c c} s \cdot cos(\pi/2) & 0 & s \cdot sin(\pi/2) & 1,244 \\ 0 & s & 0 & 2 \\ -s \cdot sin(\pi/2) & 0 & s \cdot cos(\pi/2) & 0 \\ 0 & 0 & 0 & 1 \end{array} \right) $ → $ M_{Rad1} = M_{Lok} T^{Lok}_{Rad2} $
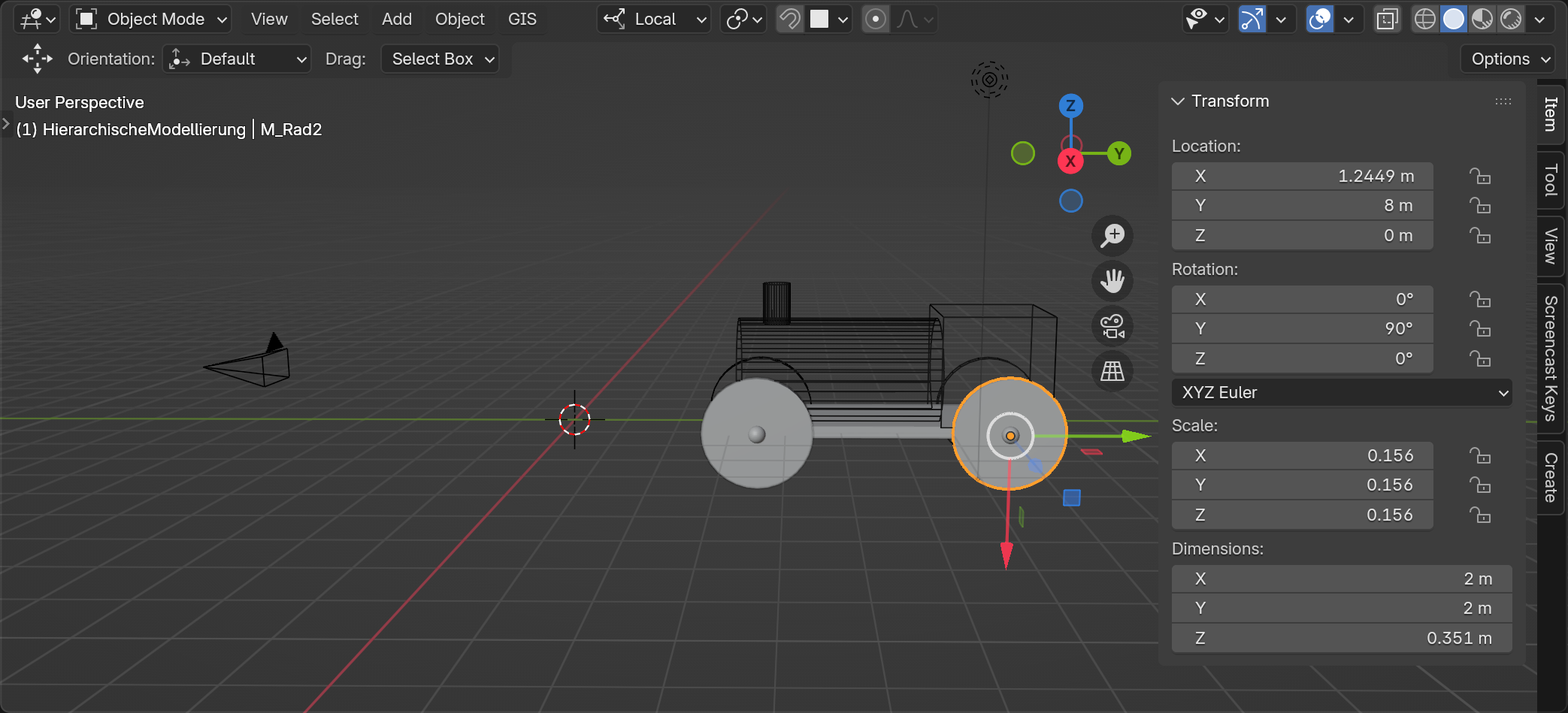
Man bezeichnet die ausmultiplizierten Matrizen f├╝r die jeweiligen Objekte, z.B. $T^{Welt}_{Lok} T^{Lok}_{Rad1}$ f├╝r Rad1, auch als Model Matrix $M_{M}$!
Probe:
T_Lok = bpy.context.scene.objects['M_Lok'].matrix_local
T_Rad1 = bpy.context.scene.objects['M_Rad1'].matrix_local
T_Rad2 = bpy.context.scene.objects['M_Rad2'].matrix_local
M_Rad1 = T_Lok @ T_Rad1
M_Rad2 = T_Lok @ T_Rad2
print(M_Rad1)
<Matrix 4x4 ( 0.0000, 0.0000, 0.1563, 1.2449)
( 0.0000, 0.1563, 0.0000, 3.5000)
(-0.1563, 0.0000, 0.0000, 0.0000)
( 0.0000, 0.0000, 0.0000, 1.0000)>
print(bpy.context.scene.objects['M_Rad1'].matrix_world)
<Matrix 4x4 ( 0.0000, 0.0000, 0.1563, 1.2449)
( 0.0000, 0.1563, 0.0000, 3.5000)
(-0.1563, 0.0000, 0.0000, 0.0000)
( 0.0000, 0.0000, 0.0000, 1.0000)>
Abschlie├čend beschreiben wir die Kamera-Transformation durch eine Verschiebung um −7 Einheiten entlang der Y-Achse und 1 Einheit entlang der Z-Achse sowie eine Rotation um 90 Grad ($\theta = \pi/2$) um die X-Achse wie folgt:
$ T^{Welt}_{Kamera} = \left( \begin{array}{c c c c} 1 & 0 & 0 & 0 \\ 0 & cos(\pi/2) & -sin(\pi/2) & -7 \\ 0 & sin(\pi/2) & cos(\pi/2) & 1 \\ 0 & 0 & 0 & 1 \end{array} \right) $
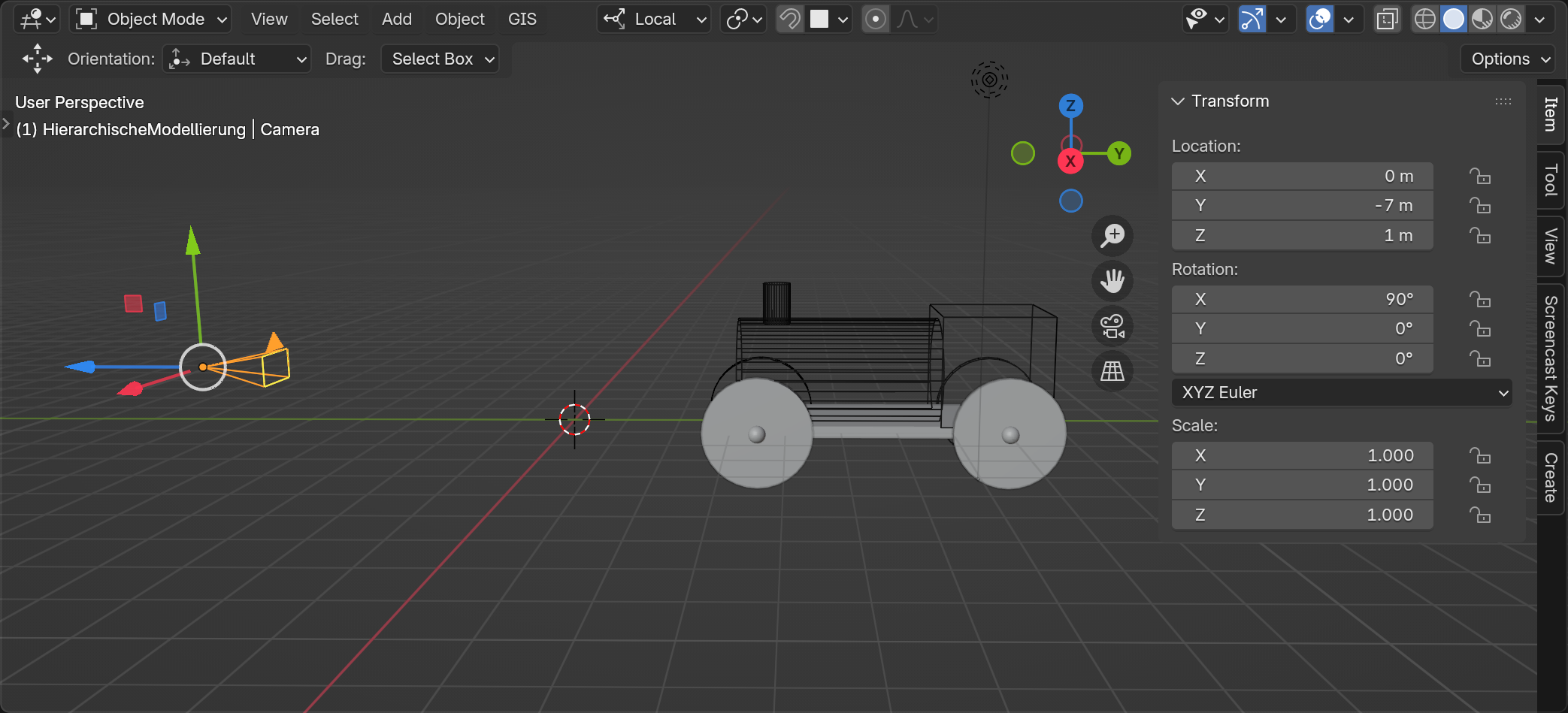
Problem: Wir ben├Âtigen die umgekehrte Transformation - von Kamerakoordinaten zu Weltkoordinaten, denn wir ben├Âtigen die Vertices nicht relativ zum zum Ursprung der Weltkoordinaten sondern relativ zum Ursprung der Kamerakoordinaten, d.h. relativ zum Augpunkt. Man nennt diese Matrix $T^{Kamera}_{Welt} = (T^{Welt}_{Kamera})^{-1}$ auch die View Matrix $M_V$
$ T^{Kamera}_{Welt} = \left( \begin{array}{c c c c} 1 & 0 & 0 & 0 \\ 0 & cos(\pi/2) & sin(\pi/2) & -1 \\ 0 & -sin(\pi/2) & cos(\pi/2) & -7 \\ 0 & 0 & 0 & 1 \end{array} \right) $
Die Gesamttransformation f├╝r das Rad1-Objekt lautet wie folgt:
Gesamtmatrix $ M_{MV} = T^{Kamera}_{Welt} \cdot T^{Welt}_{Lok} \cdot T^{Lok}_{Rad1} $
Man nennt diese Matrix auch die Model-View Matrix $M_{MV}$, die unsere Szene nun aus Kamerasicht beschreibt:
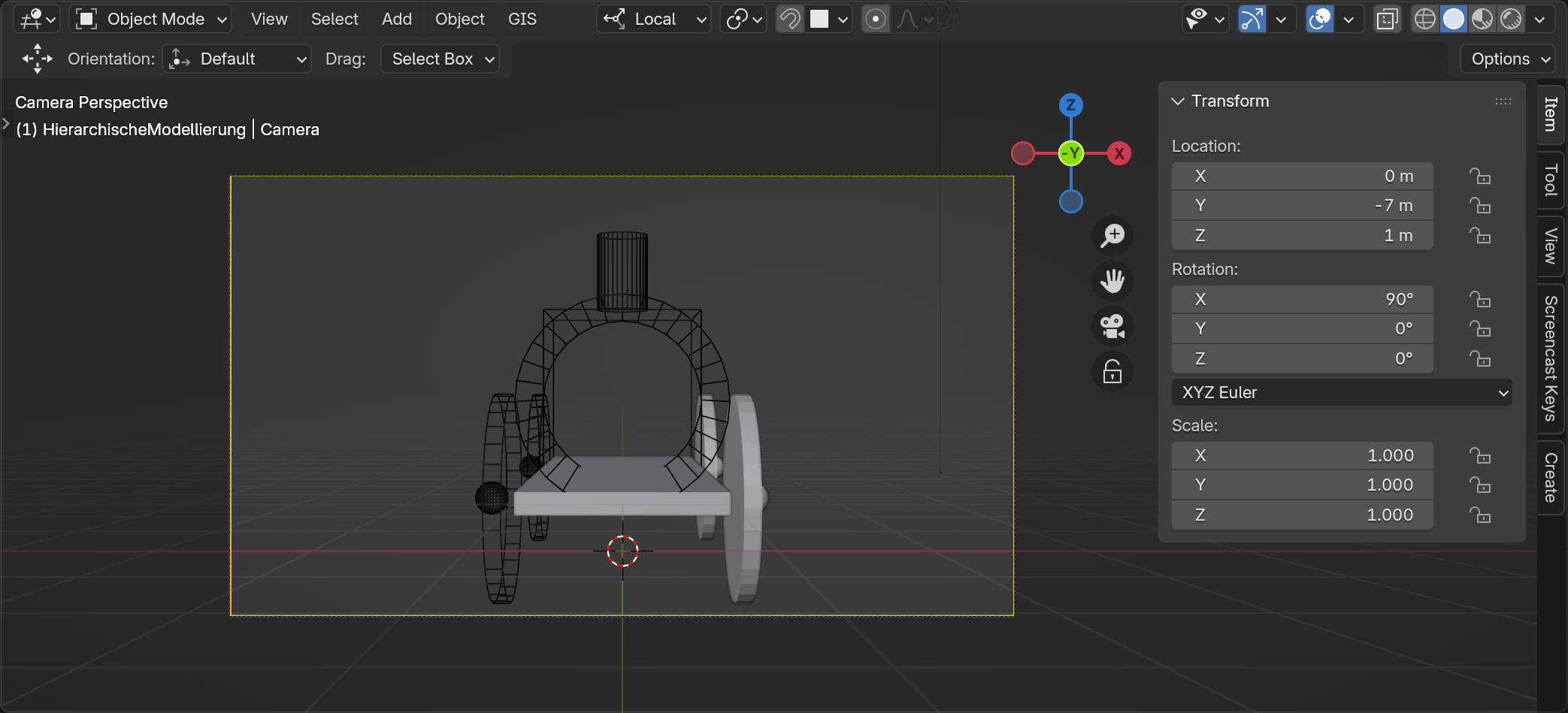
Probe:
M_V = bpy.context.scene.objects['Camera'].matrix_world.inverted()
M_MV = M_V @ M_Rad1
print(M_MV)
<Matrix 4x4 ( 0.0000, 0.0000, 0.1563, 1.2449)
(-0.1563, -0.0000, 0.0000, -1.0000)
( 0.0000, -0.1563, -0.0000, -10.5000)
( 0.0000, 0.0000, 0.0000, 1.0000)>
Laut Rechnung ist das Rad1 also 10.5 Einheiten von der Kamera entfernt. Die Kamera ist bei Y = −7 und das Rad1 ist bei Y = 3.5 → Rechnung korrekt!
Ein jedes Objekt des Szenengraphen kann nun beliebig transformiert werden, indem die Gesamttransformation (von der GPU) auf jeden Vertex angewendet wird:
Hinweis: Auch die perspektivische Projektion kann als Transformation dargestellt werden, was aus Gr├╝nden der Einfachheit hier nicht ber├╝cksichtigt wurde. Diese Transformation kommt normalerweise als letztes. Wo muss sie also hinzugef├╝gt werden?